1 齐次坐标(Homogeneous coordinates)

对于一个三维空间向量$(x,y,z)$，我们将其扩展一个维度，变成 $(x,y,z,w)$。

关于这个扩展的动机和作用后面会更加清楚，不过目前你只需要记住

• 如果 $w==1$，则向量 $(x,y,z,1)$ 表示空间中的一个位置
• 如果 $w==0$，则向量 $(x,y,z,0)$ 表示一个方向

这两种区别何在？对于旋转来说，不会有任何改变这里的不会有任何改变应该是指表示形式，第四维为0。当你旋转一个点或者一个方向的时候，会得到相同的结果这里的相同是指数学意义上的相同，作为一个向量，一个点的坐标和一个方向的数学形式是相同。采用旋转操作时，点和方向可以被认为是相同的。。但是当你做移动操作的，移动方向向量来说是没有意义的。What difference does this make ? Well, for a rotation, it doesn’t change anything. When you rotate a point or a direction, you get the same result. However, for a translation (when you move the point in a certain direction), things are different. What could mean “translate a direction” ? Not much.

齐次坐标是我们可以用同样的数学形式来处理这两种情况。

2 变换矩阵(Transformation matrices)

变换矩阵作用于向量，以矩阵乘法的形式进行，即

$$\begin{array}{}\left[\begin{array}{cccc}a& b& c& d\\ e& f& g& h\\ i& j& k& l\\ m& n& o& p\end{array}\right]\times \left[\begin{array}{c}x\\ y\\ z\\ w\end{array}\right]=\left[\begin{array}{c}ax+by+cz+dw\\ ex+fy+gz+hw\\ ix+jy+kz+lw\\ mx+ny+oz+pw\end{array}\right]& \text{(1)}\end{array}$$

2.1 位移矩阵(Translation matrices)

这是最简单的变换矩阵，形式为

$$\begin{array}{}\left[\begin{array}{cccc}1& 0& 0& X\\ 0& 1& 0& Y\\ 0& 0& 1& Z\\ 0& 0& 0& 1\end{array}\right]& \text{(2)}\end{array}$$

一个例子如下：

$$\begin{array}{}\left[\begin{array}{cccc}1& 0& 0& 10\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}10\\ 10\\ 10\\ 1\end{array}\right]=\left[\begin{array}{c}1\ast 10+0\ast 10+0\ast 10+10\ast 1\\ 0\ast 10+1\ast 10+0\ast 10+0\ast 1\\ 0\ast 10+0\ast 10+1\ast 10+0\ast 1\\ 0\ast 10+0\ast 10+0\ast 10+1\ast 1\end{array}\right]=\left[\begin{array}{c}10+0+0+10\\ 0+10+0+0\\ 0+0+10+0\\ 0+0+0+1\end{array}\right]=\left[\begin{array}{c}20\\ 10\\ 10\\ 1\end{array}\right]& \text{(3)}\end{array}$$

注意变换后的向量仍然是一个位置向量(第四维为1)。对方向向量进行变换的例子如下：

$$\begin{array}{}\left[\begin{array}{cccc}1& 0& 0& 10\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}0\\ 0\\ -1\\ 0\end{array}\right]=\left[\begin{array}{ccccccc}1\ast 0& +& 0\ast 0& +& 0\ast 0& +& 10\ast 0\\ 0\ast 0& +& 1\ast 0& +& 0\ast 0& +& 0\ast 0\\ 0\ast -1& +& 0\ast -1& +& 1\ast -1& +& 0\ast -1\\ 0\ast 0& +& 0\ast 0& +& 0\ast 0& +& 1\ast 0\end{array}\right]=\left[\begin{array}{c}0+0+0+0\\ 0+0+0+0\\ 0+0+-1+0\\ 0+0+0+0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -1\\ 0\end{array}\right]& \text{(4)}\end{array}$$

可以看到位移变换对于方向向量来说是无效的。

2.2 缩放矩阵

$$\begin{array}{}\left[\begin{array}{cccc}x& 0& 0& 0\\ 0& y& 0& 0\\ 0& 0& z& 0\\ 0& 0& 0& 1\end{array}\right]& \text{(5)}\end{array}$$

2.3 旋转矩阵

旋转矩阵的具体形式比较复杂，而在实际编程中会有成熟的框架来帮我们处理旋转矩阵，所以这里我们就不列举旋转矩阵的具体形式了。

2.4 变换累加

通过不断的矩阵左乘实现。注意旋转操作和位移操作一般不具有可交换性。

3 Model, View, Project矩阵

这三个矩阵是在三维绘图中用来清晰地分割复杂变换的工具。

3.1 Model 矩阵

三维模型是由众多的顶点(vertices)组成的，这些定点定义在以模型为原点的坐标系中。如下图

模型本身在三维空间内会有运动，例如这可能是用户通过键盘鼠标进行了操作。这部分变换通过模型矩阵来表示模型矩阵可以分解为translation*rotation*scale。我们对模型矩阵的每个顶点都乘以Model矩阵即可完成运动过程。

此时我们的顶点就从 model space 模型空间，进入了 world space，即世界空间。上面的过程可以画成如下流程图：

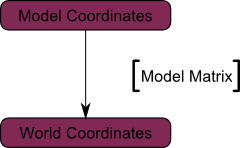
3.2 View 矩阵

The engines don’t move the ship at all. The ship stays where it is and the engines move the universe around it. ---- Futurama

上面这个引言的想法很有意思。应用同样的思想，移动摄像机(camera)的操作可以完全由移动整个世界来完成例如我们需要将摄像机向上移动 3，这个操作可以等效为将世界中的每个物体下移 3，这对于计算机图像学来说是更加简单的。

假设初始时刻我们的摄像机位于世界空间的原点，这时我们移动整个世界，让摄像机在世界中的相对位到达目标点。这个操作即为即为 View 矩阵。

经过 View 矩阵的处理，我们称模型从世界空间进入了摄像机空间(camera space)。

下面是扩展后的流程图：

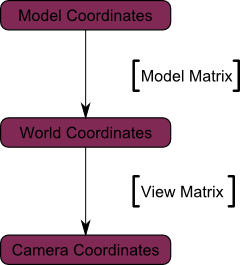
3.3 Projection 矩阵

进入摄像机空间以后，我们尚不能进行渲染，因为此时模型仍然是三维的，无法直接映射到二维图像空间。例如具有相同的x, y坐标的点，z值小的那个一个应该要更加靠近画面的中心。这个过程称为透视投影(perspective projection)。

投影的过程也可以用一个 $4\times 4$ 的矩阵来表示。

在完成投影以后，我们从摄像机空间all vertices defined relatively to the camera)来到了齐次空间all vertices defined in a small cube. Everything inside the cube is onscreen。

完整的流程图为

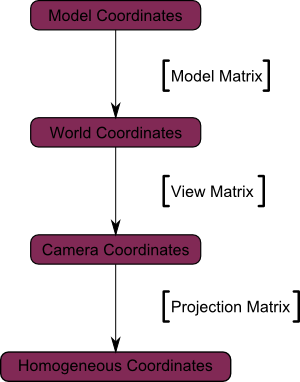
下面这个例子能更清晰地反映投影矩阵的作用：